Table of Contents
Definition of Real Numbers
Real numbers are a set of numbers that includes all rational and irrational numbers. They are called “real” because they can be represented as points on a real number line. The real number system is a continuum, meaning that there are no “gaps” or “holes” in the number line.
Here are some examples of real numbers:
- 0
- 1
- -3
- 0.5
- 2.3456789
- pi (approximately 3.14159265359)
- sqrt(2) (approximately 1.41421356237)
- e (approximately 2.71828182846)
All of these numbers are real numbers because they can be plotted on the number line, and they are not imaginary or complex numbers.
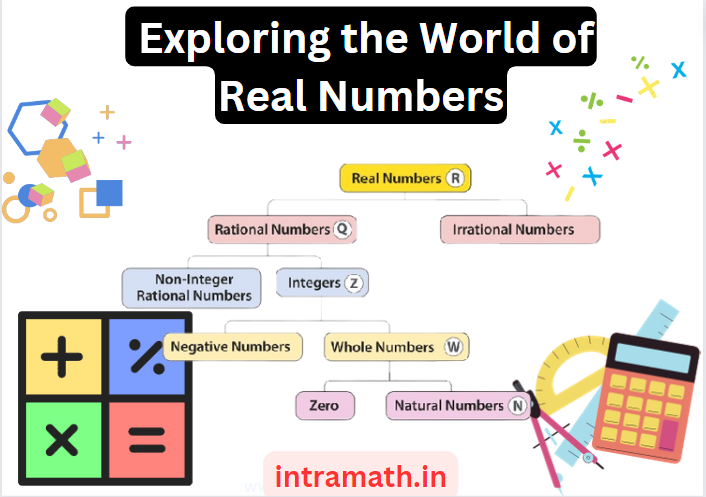
The real number system includes several subsets, including the set of natural numbers, whole numbers, integers, rational numbers, and irrational numbers. Natural numbers are the set of positive integers (1, 2, 3, …). Whole numbers are the set of non-negative integers (0, 1, 2, 3, …). Integers are the set of whole numbers and their negatives (-3, -2, -1, 0, 1, 2, 3, …). Rational numbers are the set of numbers that can be expressed as a fraction of two integers (e.g. 1/2, -3/4, 7/3). Irrational numbers are numbers that cannot be expressed as a fraction of two integers, and their decimal expansions are non-repeating and non-terminating (e.g. √2, π, e).
Real numbers can be positive, negative, or zero, and can be expressed in decimal form, as fractions, or as roots of numbers. The real number system is closed under addition, subtraction, multiplication, and division. Real numbers are used extensively in various fields of mathematics and sciences, such as geometry, calculus, physics, and engineering.
The concept of real numbers has been developed over thousands of years, with ancient civilizations like the Babylonians and Egyptians using number systems that had similarities to the modern real number system. The development of the real number system was greatly influenced by the work of ancient Greek mathematicians, such as Euclid, Pythagoras, and Archimedes. The real number system has since become a cornerstone of modern mathematics and is used in virtually every field of science and engineering.
Comparing different types of numbers:
| Type of Number | Definition | Example | Properties |
|---|---|---|---|
| Natural Numbers | Counting numbers starting from 1 | 1, 2, 3, 4, … | Closure under addition and multiplication, no additive or multiplicative inverses |
| Whole Numbers | Natural numbers including 0 | 0, 1, 2, 3, 4, … | Closure under addition and multiplication, no additive or multiplicative inverses |
| Integers | Whole numbers and their negatives | …, -3, -2, -1, 0, 1, 2, 3, … | Closure under addition and multiplication, additive and multiplicative inverses, but no closure under division |
| Rational Numbers | Numbers that can be expressed as a ratio of two integers | 1/2, -3/4, 7, 0.25 | Closure under addition, subtraction, multiplication, and division, multiplicative inverse exists for all non-zero numbers |
| Irrational Numbers | Numbers that cannot be expressed as a ratio of two integers | pi, sqrt(2), e | Not closed under any arithmetic operations, but can be approximated arbitrarily closely by rational numbers |
| Real Numbers | The set of all rational and irrational numbers | -2.5, sqrt(3), 7/11 | Closure under all arithmetic operations, includes all possible values on the number line |
| Complex Numbers | Numbers that can be expressed in the form a + bi, where a and b are real numbers and i is the imaginary unit, sqrt(-1) | 3 + 2i, -1 – 4i, 2i | Closure under all arithmetic operations, includes real numbers as a subset |
Properties of Real Numbers:
Real numbers have several important properties, including:
- Closure: The sum or product of any two real numbers is always a real number.
- Commutativity: The order of addition or multiplication of real numbers does not affect the result.
- Associativity: The grouping of addition or multiplication of real numbers does not affect the result.
- Distributivity: The distributive property holds for addition and multiplication of real numbers.
- Identity: There exist additive and multiplicative identities for real numbers.
- Inverses: Every real number has an additive and a multiplicative inverse.
- Non-zero divisor: Zero is the only real number that has no multiplicative inverse.
Sets of Real Numbers:
There are several subsets of real numbers, including:
- Natural numbers: Positive integers {1, 2, 3, …}.
- Whole numbers: Non-negative integers {0, 1, 2, 3, …}.
- Integers: Positive and negative integers {…, -2, -1, 0, 1, 2, …}.
- Rational numbers: Numbers that can be expressed as a ratio of two integers.
- Irrational numbers: Numbers that cannot be expressed as a ratio of two integers.
- Algebraic numbers: Real numbers that are roots of a polynomial equation with integer coefficients.
- Transcendental numbers: Real numbers that are not algebraic.
The Real Number Line
- The real number line is a geometric representation of the set of real numbers, with each point on the line representing a unique real number.
Absolute Value and Distance
- The absolute value of a real number is its distance from zero on the number line.
- The distance between two real numbers a and b is |a – b|.
Intervals and Inequalities
- An interval is a set of real numbers that lies between two given numbers.
- Inequalities are mathematical expressions that compare two real numbers using symbols such as <, >, ≤, and ≥.
Operations with Real Numbers
- The basic operations of addition, subtraction, multiplication, and division are defined for real numbers.
- The distributive, associative, and commutative properties hold for these operations.
Applications of Real Numbers
- Real numbers are used extensively in mathematics, science, engineering, and finance to model and solve problems.
- They are used to measure physical quantities such as length, time, temperature, and weight, as well as to represent quantities in abstract systems.
Complex Numbers and Imaginary Numbers
- Complex numbers are numbers that can be written in the form a + bi, where a and b are real numbers and i is the imaginary unit, which is defined as the square root of -1.
- Imaginary numbers are complex numbers with a real part of zero. They are denoted by bi, where b is a non-zero real number.
Here’s an example of a table comparing complex and imaginary numbers:
| Property | Complex Numbers | Imaginary Numbers |
|---|---|---|
| Definition | Numbers of the form a + bi, where a and b are real numbers and i is the imaginary unit, defined as i^2 = -1 | Numbers of the form bi, where b is a non-zero real number and i is the imaginary unit, defined as i^2 = -1 |
| Real and Imaginary Parts | Has both real and imaginary parts | Has only an imaginary part |
| Graphical Representation | Plotted on a complex plane, with the real part as the x-axis and the imaginary part as the y-axis | Not plotted on a complex plane, but can be represented as a point on the y-axis of a coordinate plane |
| Arithmetic Operations | Addition, subtraction, multiplication, division, and exponentiation are defined | Addition and subtraction are defined, but multiplication and division are not defined |
| Examples | 2 + 3i, -5i, 1 – i√3 | 5i, -2i, πi |
Mathematics all Number System Topics sarkari schools website there you can find all topics in hindi
What are Natural and Real Numbers?
Natural numbers are all positive integers starting from 1 to infinity. All natural numbers are integers but not all the integers are natural numbers. These are the set of all counting numbers such as 1, 2, 3, 4, 5, 6, 7, 8, 9, …….∞.
Real numbers are numbers that include both rational and irrational numbers. Rational numbers such as integers (-2, 0, 1), fractions(1/2, 2.5) and irrational numbers such as √3, π(22/7), etc., are all real numbers.
Is Zero a Real or an Imaginary Number?
Zero is considered to be both a real and an imaginary number. As we know, imaginary numbers are the square root of non-positive real numbers. And since 0 is also a non-positive number, therefore it fulfils the criteria of the imaginary number. Whereas 0 is also a rational number, which is defined in a number line and hence a real number.
Are there Real Numbers that are not Rational or Irrational?
No, there are no real numbers that are neither rational nor irrational. The definition of real numbers itself states that it is a combination of both rational and irrational numbers.
Is the real number a subset of a complex number?
Yes, because a complex number is the combination of a real and imaginary number. So, if the complex number is a set then the real and imaginary numbers are the subsets of it.
What are the properties of real numbers?
The properties of real numbers are:
Commutative Property
Associative Property
Distributive Property
Identity Property
Is √3 a real number?
Yes, √3 is a real number. We know that a real number is a combination of both rational and irrational numbers. Since √3 is an irrational number, we can also say that √3 is a real number.
Is 3i a real number?
No, 3i is not a real number, as it has an imaginary part in it.
What are the different subsets of real numbers?
The subsets of real numbers include rational numbers, irrational numbers, natural numbers, and whole numbers.
What are real numbers?
A: Real numbers are the set of numbers that include both rational and irrational numbers. They can be plotted on a number line and include all possible values.
What is the difference between a real number and a complex number?
A: A real number is a number that can be plotted on the number line, while a complex number is a number that includes an imaginary component, usually represented as a+bi, where a and b are real numbers.
What is the absolute value of a real number?
A: The absolute value of a real number is the distance of that number from 0 on the number line. It is always positive or 0.
What is the difference between a rational number and an irrational number?
A: A rational number is a number that can be expressed as a ratio of two integers, while an irrational number cannot be expressed as a ratio of two integers.
Can every real number be expressed as a decimal?
A: Yes, every real number can be expressed as a decimal, but not all decimals are terminating or repeating.
What is the decimal expansion of pi?
A: The decimal expansion of pi is an infinite, non-repeating decimal that starts with 3.14159…
How do you add and subtract real numbers?
A: To add or subtract real numbers, you line up the decimal points and then add or subtract the digits in each place value. If necessary, you may need to carry or borrow.
What is the order of operations for real numbers?
A: The order of operations for real numbers is Parentheses, Exponents, Multiplication and Division (from left to right), and Addition and Subtraction (from left to right).
What is a rational approximation of an irrational number?
A: A rational approximation of an irrational number is a rational number that is very close to the irrational number, but not exactly equal. For example, 22/7 is a rational approximation of pi.
What is the difference between a real number and an imaginary number?
A: A real number is a number that can be plotted on the number line, while an imaginary number is a number that is a multiple of the imaginary unit i, which is defined as the square root of -1.
What is the value of “x” in the equation x^2 = -4?
A: There is no real number that satisfies this equation, because the square of any real number is always non-negative.
What is the decimal representation of 1/3?
A: The decimal representation of 1/3 is an infinite, non-repeating decimal that starts with 0.33333…
Is the number 0.999… equal to 1?
A: Yes, the number 0.999… is equal to 1, because they represent the same value on the number line.
What is the largest real number?
A: There is no largest real number, because the set of real numbers is infinite and unbounded.
What is the smallest real number?
A: There is no smallest real number, because the set of real numbers is infinite and unbounded.
What is the sum of all real numbers?
A: The sum of all real numbers does not exist, because the set of real numbers is infinite and unbounded.
What is the difference between 0 and -0?
A: There is no difference between 0 and -0, because they represent the same value on the number line.
What is the opposite of infinity?
A: Infinity is not a real number, so it does not have an opposite in the usual sense.
What is the square root of -1?
A: The square root of -1 is an imaginary number, usually denoted as i.
Can a real number be both positive and negative?
A: No, a real number cannot be both positive and negative at the same time. However, it can be either positive or negative, or it can be 0.
परिषदीय विद्यालयों की अवकाश तालिका Download Holidays List …
Basic Shiksha Parishad avkash talika 2023
Download Holidays List Basic Shiksha Parishad 2023 Pdf.
